Conditional Statements

In conditional statements, "If p then q" is denoted symbolically by "p q"; p is called the hypothesis and q is called the conclusion. For instance, consider the two following statements:

If Sally passes the exam, then she will get the job.

If 144 is divisible by 12, 144 is divisible by 3.

Let p stand for the statements "Sally passes the exam" and "144 is divisible by 12".
Let q stand for the statements "Sally will get the job" and "144 is divisible by 3".

The hypothesis in the first statement is "144 is divisible by 12", and the conclusion is "144 is divisible by 3".

The second statement states that Sally will get the job if a certain condition (passing the exam) is met; it says nothing about what will happen if the condition is not met. If the condition is not met, the truth of the conclusion cannot be determined; the conditional statement is therefore considered to be vacuously true, or true by default.

D E F I N I T I O N S

Let p and q be statement variables which apply to the following definitions.

Conditional:	The conditional of q by p is "If p then q" or "p implies q" and is denoted by p q. It is false when p is true and q is false; otherwise it is true.
Contrapositive:	The contrapositive of a conditional statement of the form "If p then q" is  "If  ~q then  ~p".  Symbolically, the contrapositive of p q is ~q~p. A conditional statement is logically equivalent to its contrapositive.
Converse:	Suppose a conditional statement of the form "If p then q" is given. The converse is "If q then p." Symbolically, the converse of p q is q p. A conditional statement is not logically equivalent to its converse.
Inverse:	Suppose a conditional statement of the form "If p then q" is given. The inverse is "If ~p then ~q." Symbolically, the inverse of p q is ~p ~q. A conditional statement is not logically equivalent to its inverse.
Only if :	p only if q means "if not q then not p, " or equivalently, "if p then q."
Biconditional (iff):	The biconditional of p and q is "p if, and only if, q" and is denoted p q. It is true if both p and q have the same truth values and is false if p and q have opposite truth values.
Sufficient condition:	p is a sufficient condition for q means "if p then q."
Necessary condition:	p is a necessary condition for q means "if not p then not q."

In expressions that include and other logical operators such as , , and ~, the order of operations is that is performed last while ~ is performed first.

Representation of If-Then as Or

Let ~p be "You do your homework" and q be "You will flunk".  The given statement is "Either you do your homework or you will flunk", which is ~p q.  In if-then form, p q means that "If you do not do your homework, then you will flunk", where p (which is equivalent to ~~p ) is "You do not do your homework".

p q ~p q

The negation of a conditional statement is represented symbolically as follows:

~(p q) p ~q

By definition, p q is false if, and only if, its hypothesis, p, is true and its conclusion, q, is false.

The converse and inverse of a conditional statement are logically equivalent to each other, but neither of them are logically equivalent to the conditional statement

Practice Exercises

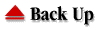Truth Table For Conditional Statements

p	q	p q	q p	p q	(p q) (q p)
T	T	T	T	T	T
T	F	F	T	F	F
F	T	T	F	F	F
F	F	T	T	T	T