Set Properties
and Definitions
Set Properties | Set
Definitions | Set Equality | The
Empty Set
Set Partitions and Power Sets
| Boolean Algebras
Set Properties
Given sets A, B, and C, and a universal set U,
the following properties hold:
Set Definitions
Given a universal set U, let A and B
be subsets of U, and x and y be elements
of U. Then,
- x
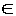 A
A 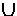 B
B
 x
x
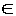 A or
x
A or
x 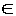 B
B
- x
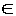 A
A 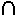 B
B
 x
x
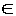 A and
x
A and
x 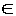 B
B
- x
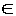 A - B
A - B
 x
x
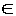 A and
x
A and
x 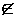 B
B
- x
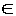 Ac
Ac x
x
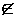 A
A
- (x, y)
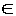 A
x B (the cross product)
A
x B (the cross product) x
x
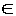 A and
y
A and
y  B
B
 Practice Exercises
Practice Exercises |
 |
Set Equality
Given sets X and Y, the two sets are equal (X =
Y) iff every element of X is in Y, and every
element of Y is in X.
Drawing from the earlier definition of subsets,
set equality can be represented symbolically as follows:
X = Y  X
X
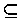 Y
and Y
Y
and Y 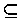 X.
X.
The Empty Set
Earlier, we touched on the concept of an "empty set", a set
with no elements. Just as it is possible and even necessary to use
'0' in mathematics, or to speak of 'nothing' or 'nobody' in daily conversation,
so is the concept of an empty set necessary to set theory.
The following theorem and corollary deal with properties of the empty
set.
Theorem: The Empty Set is a subset of every other set.
Corollary: There is only one empty set. (The empty set
is unique.)
Set Partitions and
Power Sets
Disjoint Sets
Two sets which have no elements in common are called disjoint,
defined symbolically as follows:
A and B are disjoint  A
A
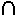 B =
B = 
Mutually Disjoint Sets
Let A = {1, 2, 3, 4, 5, 6, 7, 8, 9}. Suppose that A
is divided into the following:

A1 = {1, 2, 3},
A2 = {4, 5, 6}, and
A3 = {7, 8, 9}.
The collection of these subsets, {A1, A2, A3},
is a partition of set A, and A
is a union of mutually disjoint subsets.
The sets A1, A2, A3, . . ., An are
said to be mutually disjoint iff, for all i, j = 1, 2, 3, ..., n,
Ai 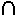 Aj
=
Aj
= whenever
i
whenever
i 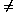 j.
j.
Power Sets
Let X = {a, b, c}. The power set of X, denoted P(X),
is the set consisting of all subsets of X. For this example,
P(X) = { ,
{a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}.
,
{a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}.
Power sets have the following 2 properties:
For all sets X and Y, if X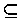 Y,
then P(X)
Y,
then P(X)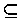 P(Y).
P(Y).
If a set X has n elements, then P(X) has
2n elements.
 Practice Exercises
Practice Exercises |
 |
Boolean
Algebras
Boolean algebra is a particular algebraic method
used to determine the truth or falsity of statements. It uses 2 operators,
generally denoted as + (addition) and x (multiplication),
and given a set S with elements a and b,
both a + b and a x b
are in S. The operations performed by 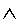 and
and
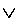 upon statement forms,
and the set theory operations performed by
upon statement forms,
and the set theory operations performed by 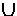 and
and
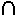 are specialized
forms of Boolean algebras. The similarities can be seen in the following
table.
are specialized
forms of Boolean algebras. The similarities can be seen in the following
table.
Boolean
Algebra |
Statement
Algebra |
Set
Theory |
English
Equivalent |
| + |
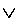 |
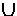 |
"or" |
| x |
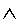 |
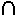 |
"and" |
| 0 |
F |
|
"false" |
| 1 |
T |
|
"true" |
| a' |
~a |
ac |
"not a" |
Likewise, similarities can be seen in the properties
of statement algebra, set
theory properties and Boolean algebra. Given a set S, with
elements a, b and c, the following
axioms are true:
| 1. |
Commutative property: |
a + b = b + a
a x b = b x a
|
| 2. |
Associative property: |
(a + b) + c = a + (b + c)
(a x b) x c = a x (b x c)
|
| 3. |
Distributive property: |
a + (b x c) = (a + b) x (a + c)
a x (b + c) = (a x b) + (a x c)
|
| 4. |
Identity properties: |
a + 0 = a
a x 1 = a
|
| 5. |
Complementation properties: |
a + a' = 1
a x a' = 0
|