Argument Forms
D E F I N I T I O N S
| Argument |
A series of statements . |
| Premises |
All statements in an argument except the final one. |
| Conclusion |
The final (or concluding) statement in an argument. |
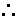 |
Symbol for "therefore", normally used to
identify the conclusion of an argument. |
| Modus Ponens |
Latin for "method of affirming." A rule
of inference used to draw logical conclusions, which states that if p
is true, and if p implies q (p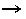 q),
then q is true. q),
then q is true. |
| Modus Tollens |
Latin for "method of denying." A rule of
inference drawn from the combination of modus ponens and the contrapositive.
If q is false, and if p implies q
(p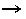 q),
then p is also false. q),
then p is also false. |
| Fallacy |
An error in reasoning. |
| Contradiction Rule |
Given a statement p, if ~p
leads logically to a contradiction, then p must be true. |
Testing For Argument
Validity
As shown in earlier, the content of a statement or argument can be represented
in a logical form by the use of statement variables. For example:
| If I study hard, then I will get an A. |
|
p 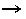 q q |
| I will study hard. |
|
p |
| Therefore, I will get an A. |
 |
q |
An argument form is valid if, no matter what statements are substituted
for the premises statement variables, if the premises are all true, then
the conclusion is also true. The truth of the conclusion must follow necessarily
from the truth of the premises.
To determine an argument's validity:
- Identify the premises and conclusion of the argument.
- Create a truth table showing the values of the premises and conclusion.
- Locate the rows in which the premises are all true (the critical
rows).
- For each critical row, determine if the conclusion is also true.
If the conclusion is true for each critical row, then the argument form
is valid. But if even one of the critical rows contains a false conclusion,
the argument is invalid.
 Practice Exercises
Practice Exercises |
 |
Modus Ponens and
Modus Tollens
These 2 methods are used to prove or disprove arguments, Modus Ponens
by affirming the truth of an argument (the conclusion becomes the
affirmation), and Modus Tollens by denial (again, the conclusion
is the denial). Consider the following argument:
If it is bright and sunny today, then I will wear
my sunglasses.
| Modus Ponens |
Modus Tollens |
| It is bright and sunny today. |
I will not wear my sunglasses. |
| Therefore, I will wear my sunglasses. |
Therefore, it is not bright and sunny today. |
Construction of a truth table will show that these
two argument forms are equivalent, and further demonstrates the fact that a
conditional statement is logically equivalent to its contrapositive.
 Practice Exercises
Practice Exercises |
 |
Other Valid Argument Forms
The following additional argument forms are valid.
|
|
Example 1 |
|
|
Example 2 |
| Disjunctive Addition | |
p |
|
|
q |
|
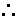 |
p  q q |
|
 |
p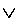 q q |
|
|
|
|
|
|
| Conjunctive Simplification | |
p 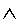 q q |
|
|
p 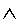 q q |
|
 |
p |
|
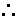 |
q |
|
|
|
|
|
|
| Disjunctive Syllogism | |
p 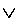 q q |
|
|
p 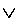 q q |
|
|
~q |
|
|
~p |
|
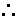 |
p |
|
 |
q |
|
|
|
|
|
|
| Hypothetical Syllogism | |
p  q q |
|
|
|
|
|
q  r r |
|
|
|
|
 |
p 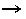 r r |
|
|
|
|
|
|
|
|
|
| Proof by Division into Cases | |
p 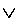 q q |
|
|
|
|
|
p 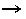 r r |
|
|
|
|
|
q 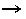 r r |
|
|
|
|
 |
r |
|
|
|
Common Fallacies
An error in logic or reasoning is called a fallacy, and the result of
such errors is an invalid argument. The three most common fallacies are:
- Vague or ambiguous premises
- Begging the question (assuming what is to be proven)
- Jumping to conclusions (using inadequate logic or premises)
Two other reasoning errors which are common are:
Converse Error
Converse error resembles modus ponens (which is why it's such
an easy mistake to make!). Consider the following absurd example:
If someone kicks me, I will yell "ouch!"
I just yelled "ouch!".
Therefore, someone kicked me.
It is logical to presume that, if someone decides to kick you, your
reaction would be a pained yelp. However, the fact that you yelled "ouch"
does not necessarily mean that the nearest bystander walked up and kicked
you. (You also might yell if you pricked yourself with a pin, dropped a
hammer on your foot, or received a "D" on a test paper.)
Inverse Error
Like the above converse error, inverse error also appears very similar
to a valid argument form - the contrapositive.
If I hit my professor with a cream pie, he will flunk me.
I will not hit my professor with a cream pie.
Therefore, he will not flunk me.
Again, it is intuitively obvious that this reasoning does not work. While many
professors may consider being nailed with a cream pie a sufficient
reason to assign a grade of "F" to a student, there are an
overwhelming number of other reasons for which you might flunk (cheating,
not studying, not showing up for tests, etc.).
Be aware that a valid argument may have a false conclusion, particularly if
the premises are false. Likewise, an invalid argument may result in a true conclusion.
The Contradiction Rule
The contradiction rule is the basis of the proof by contradiction method.
The logic is simple: given a premise or statement, presume that the statement
is false. If this presumption leads to a contradiction, then the given
statement must be true. Consider the following:
All even integers are divisible by 2.
But suppose not; suppose there is a number that is even and is not divisible
by 2.
There is no such number. (The contradiction.)
Therefore, the original premise is true.