The Abacus:The Art of Calculating with Beads
Luis Fernandes
Operate the abacus that appears below by click and releasing (not dragging)
the mouse-pointer on the beads; the value for each column will update.
Note: There was a problem with one of the images (nodiamond) which
caused the abacus to malfunction (I bet the Chinese didn't have this
problem way back when it was invented); it should be OK now.
Aug 1, 1995: Finally got some more time to work on the abacus...
Magic is fun, but it's always more fun to know how it's all done.
When complete, this will be a tutorial on using the abacus. Until
then, enjoy what is here and look forward to what is yet to come.
 WHAT'S NEW...
WHAT'S NEW...
- overflow indicated by changing the display-color of the value to red and
prefixing the value with an "*" (Aug 1, 1995);
TODO...
Handle carry and overflow between columns; the
addition/subtraction tutorial.
1.0 Introduction: The Anatomy of an Abacus
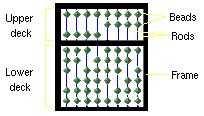 FIGURE 1:The Anatomy of an Abacus
FIGURE 1:The Anatomy of an Abacus
The classic abacus has two decks. Each deck, separated by a beam, has
several (normally 13) rods on which are mounted beads. Each rod on the
top deck contains 2 beads, and each rod on the bottom deck contains 5
beads. Each bead on the upper deck has a value of five, while each
bead on the lower deck has value of one. Beads are considered
counted, when moved towards the beam that separates
the two decks.
FIGURE 2:Numeric representation of the number: 87,654,321
Figure 2 is also a java-applet. It specifies the initial configuration
using the VALUE resource.
The first column representing the number 8, is composed of 1 bead from
the top-column (value 5) and 3 beads from the bottom-column
(each with a value of 1, totaling 3); the sum of the column
(5+3) is 8.
Similarily, the second column representing the number 7, is composed
of 1 bead from the top-column (value 5) and 2 beads from the
bottom-column (each with a value of 1, totaling 2); the sum
of the column (5+2) is 7.
2.0 Addition
Addition on the abacus involves registering the numbers on the beads
in the straight-forward left-to-right sequence they are written down
in. As long as the digits are placed correctly, and the carry's noted
properly, the answer to the operation immediately presents itself
right on the abacus. There are 4 approaches to performing additions
(or subtractions), each applied to particular situations. Each of
these techniques is explained in tabular form in the sections that
follow.
2.1 Simple Addition
When performing the addition 6+2, one would move 1 bead from the upper
deck down (value = 5) and one bead from the lower deck up (value = 1);
this represents 6. Moving 2 beads from the lower deck (in the same
column) up (value = 1 * 2 beads = 2) would complete the operation. The
answer is then obtained by reading resultant bead positions.
2.2 Combined Adding-up And Taking Off
When the original number registered on a rod is smaller than 5, but
will become greater than 5 after the addition, one bead from the
upper-deck is moved down (added on to the beam) and one or more beads
from the lower deck removed from the beam.
When a sum greater than 10 occurs on a certain rod, beads are removed
from either or both the upper and lower decks and 1 bead is added to
the rod directly to the left. Example: When adding 9 (10-1) to 8, one
bead from the lower deck is removed (-1) and one bead from the lower
deck on the row directly to the left is added (+10).
2.4 Combined Adding-up, Taking-off And Place Advancement
There are 4 cases when beads are added to the lower-deck, removed from
the upper-deck and one bead added to the adjacent rod. Example: When
adding 7 to 6 (+1-5+10), one bead is added to the lower-deck, one bead
removed from the upper-deck and one bead is added to the left rod
(lower-deck).
3.0 Subtraction
Subtraction is performed by first registering the minuend and then
subtracting, starting from the left, by removing beads form either or
both the lower or upper decks. The final bead-positions represent the
answer.
3.1 Simple Taking-off
This is achieved by simply taking off one or more beads from the lower
deck, or sometimes both. Example: When subtracting 7 (represented by
-5-2= -7) from 9, remove 1 bead from the upper-deck (-5) and 2 beads
from the lower deck (-2). The remaining 2 beads represent the result.
3.2 Combined Adding-up And Taking Off
When the number of beads in the lower deck is less than the subtracter
(the number being subtracted), one or more beads are added in the
lower deck and 1 bead is removed from the upper-deck.
Example: When subtracting 4 (+1-5 = -4) from 7 (represented by 1 bead
in the upper-deck and 2 beads in the lower deck (less than 4, the
subtracter), one bead is added to the lower deck (+1) and 1 bead is
removed from the upper-deck (-5) leaving 3 beads, representing the
result.
3.3 Taking-off From A Rod Of Higher Order And Adding-up
When a number on a specific rod is smaller than the subtrahend (4 is
the subtrahend when performing 13 - 4; note that in the ones column,
the 3 is less than the 4) one bead for the order of tens and one bead
from the lower-deck has to be taken off, and one bead from the
upper-deck is counted.
3.4 Combined Taking-off From A Rod Of Higher Order, Adding-up in the Upper-deck and Taking-off in the Lower-Deck
This technique is called for when a number on a specific rod is
smaller than the supposed subtrahend (I have no idea what this means),
but only in such cases as exemplified by 12 - 6.
If you've actually read this user's guide up to this point,
hoping to learn how to use the abacus to its maximum potential, I
should tell you that you'd be better off using a hand-held (or pop-up)
digital calculator. (I hear you asking: Why did I bother going through
all this if I was going to expound this heresy at the conclusion?
Essentially, the exercise was designed to be didactic; from my
programming stand-point, it was an interesting program to attempt and
hopefully, the user would learn a thing or two (admit it, you now know
how an abacus works). Unquestionably, though, it was unmitigated
fun!).
Technically, the abacus is a hand-held digital calculator, but that
the user must perform some sort of arithmetic manipulations before the
solution is arrived at.
4.0 Acknowledgments
The original version of this this very same program is archived
somewhere on the net as xabacus.
A great debt of gratitude goes to Agustine Lee, instructor at the
Ryerson Electrical and
Computer Engineering Department, who supplied a real, live abacus
without which xabacus would not be possible, for supplying invaluable
documentation, that was shamelessly plagiarized into the documentation
you are now reading, for the Chinese characters, and for testing
xabacus and providing helpful comments on improving
it....
...thanks also to Nick Colonello, former sysadmin at EE and all-round
technical-support person, for beta testing....
...and to Eva Dudova, who has expertise in unmercifully crashing
applications (has a future as a beta-tester), and is cute too...
... and finally, thanks to those who have written X-applications and
the demo Java applets, from whose code I have learned the art of X and Java.
The beads for the abacus, were generated using the Interactive WWW graphics
generator. Check it out!
5.0 Do those Chinese characters really mean anything?
A few people have asked me this, so here's the translation:
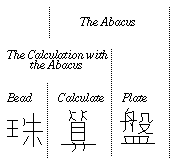
The Abacus: The Art of Calculating with Beads/ Luis Fernandes elf@ee.ryerson.ca

 WHAT'S NEW...
WHAT'S NEW...
 FIGURE 1:The Anatomy of an Abacus
FIGURE 1:The Anatomy of an Abacus 